The Bloom Filter addresses the existence-checking problem for massive datasets. It’s particularly suitable for scenarios requiring determination of data presence with tolerable minor errors (e.g., cache penetration, large-scale deduplication).
If unfamiliar, consider this example:
There are 100 bottles of liquid, one of which is poison—just a single drop can kill a mouse within 24 hours. How can you identify the poisoned bottle in one day using the fewest mice?
Some might suggest using 100 mice, but why sacrifice an entire rodent family? The solution is simple: only 7 mice are needed, leveraging binary encoding in mathematics.
Step-by-Step Solution Using Binary Encoding
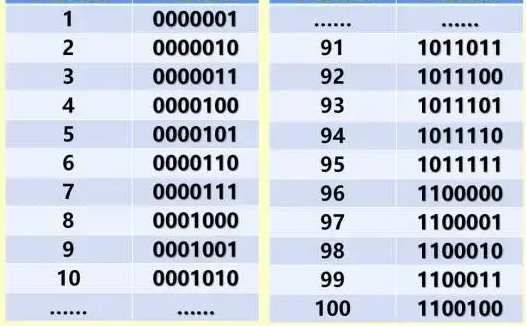
Step 1: Encode the 100 bottles from 1 to 100, then convert them into 7-bit binary codes (explained later). For example:
- Bottle 1 →
0000001 - Bottle 10 →
0001010
Step 2: Assign each of the 7 mice a unique number (1–7). Feed each mouse the bottles where their corresponding binary digit is 1:
- Mouse 1: Bottles with the 1st bit as
1 - Mouse 2: Bottles with the 2nd bit as
1 - …and so on.
Step 3: After 24 hours, observe which mice die:
- A dead mouse indicates the poison bottle’s binary digit at that position is
1. - A surviving mouse means the digit is
0.
If Mice 2, 4, 5, and 7 die, the poison bottle’s binary code is 0101101 (Decimal: Bottle 45).
This demonstrates that locating an element among 100 requires only 7 ≥ log₂100 bits—the core principle behind Bloom Filters.
Implementation
A Bloom Filter uses a bit array where each element occupies 1 bit (0 or 1), enabling extreme memory efficiency. For instance:
- A 1-million-element array consumes just 122KB.

Pros: High efficiency and performance.
Cons:
- Non-zero false-positive rate.
- Difficult to delete elements.
- False positives increase with more elements.
Core Operations
Adding an Element:
- Compute multiple hash values for the element.
- Set the corresponding bit array indices to
1.
Checking Existence:
- Recompute the same hashes.
- If all corresponding bits are
1, the element likely exists. If any bit is `0**, it *definitely* doesn’t.

Key Notes:
- Hash collisions may occur (mitigated by adjusting array size/hash functions).
- “Exists” → May be wrong; “Not exists” → Always correct.
Python Implementation
from bitarray import bitarray
import mmh3
class BloomFilter(set):
def __init__(self, size, hash_count):
super().__init__()
self.bit_array = bitarray(size)
self.bit_array.setall(0)
self.size = size
self.hash_count = hash_count
def add(self, item):
for i in range(self.hash_count):
index = mmh3.hash(item, i) % self.size
self.bit_array[index] = 1
return self
def __contains__(self, item):
return all(self.bit_array[mmh3.hash(item, i) % self.size] for i in range(self.hash_count))
# Usage
bloom = BloomFilter(100, 10)
urls = ['www.baidu.com', 'www.qq.com', 'www.jd.com']
for url in urls:
bloom.add(url)
print("www.baidu.com" in bloom) # True
print("www.fake.com" in bloom) # False (or rarely, True)Redis Integration for Distributed Systems
For persistent or distributed use (e.g., multi-node crawlers), store the bit array in Redis:
- Install Redis:
pip install redis- Example:
import redis
r = redis.Redis(host='localhost', port=6379, db=0)
r.execute_command('BF.RESERVE', 'myBloomFilter', 0.01, 100000) # Create filter
# Add/check items
items = ['url1', 'url2']
for item in items:
r.execute_command('BF.ADD', 'myBloomFilter', item)
print(r.execute_command('BF.EXISTS', 'myBloomFilter', 'url1')) # 1 (True)Distributed Workflow: Replace localhost with a shared Redis server IP to synchronize deduplication across nodes.
